Have you ever wondered why some numbers are like “lone wolves” that can’t be broken down into smaller pieces? In the world of Mathematics, these are called Prime Numbers.
Whether you are a student preparing for an exam or just someone curious about how numbers work, this guide will make everything crystal clear. We will explore prime numbers between 1 to 100, dive into the mystery of twin primes, and even look beyond 100!
What Exactly is a Prime Number?
Let’s keep it simple: A prime number is a whole number greater than 1 that has only two “friends” (factors): 1 and itself. For example, take the number 5. You can only get 5 by multiplying 1 times 5. No other whole numbers work! That makes it a Prime Number. On the other hand, a number like 6 can be $2 \times 3$, so it is NOT prime (it’s called a Composite Number).
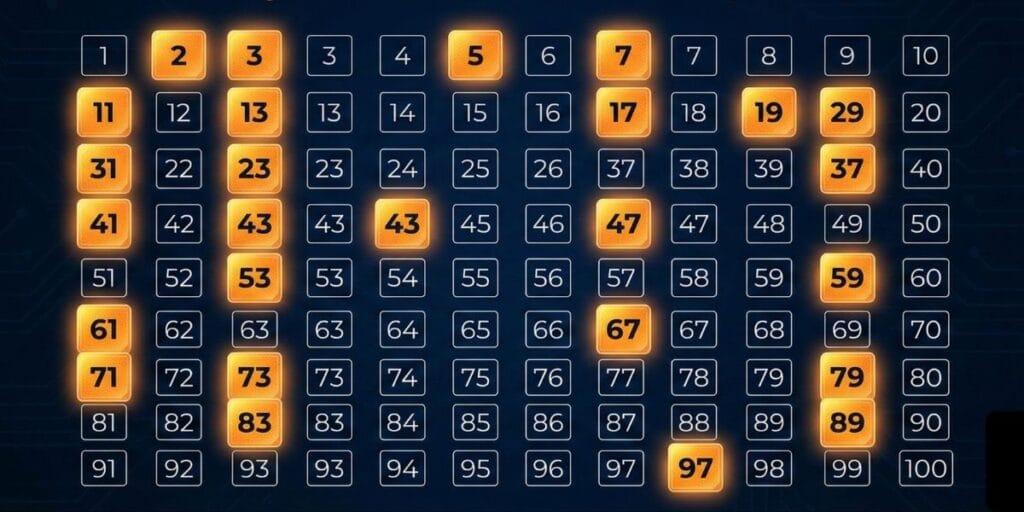
All Prime Numbers Between 1 to 100 (The Master List)
There are exactly 25 prime numbers between 1 and 100. Here they are, grouped for easy memorizing: Ever felt like some numbers are just… exclusive? In the world of mathematics, prime numbers are the ultimate “lone wolves.” They are the building blocks of all other numbers, yet they refuse to be broken down themselves.
Simply put, a prime number is a whole number greater than 1 that cannot be divided exactly by any other number except 1 and itself. For example, 7 is a prime because you can only get it by multiplying $1 \times 7$. But 8 is not prime, because $2 \times 4$ also equals 8.
Whether you are a student trying to ace your next math test, a competitive exam aspirant, or just someone who loves the logic of numbers, mastering the prime numbers between 1 to 100 is a fundamental skill. Out of the first hundred numbers, only 25 hold this special prime status.
| Range | Prime Numbers |
| 1 – 10 | 2, 3, 5, 7 |
| 11 – 20 | 11, 13, 17, 19 |
| 21 – 30 | 23, 29 |
| 31 – 40 | 31, 37 |
| 41 – 50 | 41, 43, 47 |
| 51 – 60 | 53, 59 |
| 61 – 70 | 61, 67 |
| 71 – 80 | 71, 73, 79 |
| 81 – 90 | 83, 89 |
| 91 – 100 | 97 |
Quick Fact: 2 is the only even prime number. Every other prime number is odd!
Why are some numbers missing? (80 to 100 Deep Dive)
Many people search specifically for prime numbers between 80 to 100. In this range, many numbers look prime but aren’t.
- 83 (Prime)
- 89 (Prime)
- 97 (Prime)
Wait, what about 91? Many students think 91 is prime. But if you divide 91 by 7, you get 13! So, 91 is a “trick” number – it’s composite, not prime.
Twin Prime Numbers Between 1 to 100
What are twin prime numbers? These are pairs of prime numbers that have a difference of exactly 2. They are like “neighbors” with just one even number sitting between them.
The Twin Prime pairs between 1 to 100 are:
- (3, 5)
- (5, 7)
- (11, 13)
- (17, 19)
- (29, 31)
- (41, 43)
- (59, 61)
- (71, 73)
Prime Numbers Between 100 to 200
If you’ve mastered the first 100, you might be curious about the next set. There are 21 prime numbers in the 100-200 range:
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
How to Identify Prime Numbers (The Expert Way)
Identifying prime numbers doesn’t have to be a guessing game. While some numbers like 7 or 11 are easy to spot, others like 91 or 97 can be tricky. To find these “lone wolves” quickly, we use one of the oldest and most reliable methods in history.
- Write 1-100: Cross out 1 (it’s neither prime nor composite).
- Circle 2: Cross out all multiples of 2 (4, 6, 8…).
- Circle 3: Cross out all multiples of 3 (9, 12, 15…).
- Circle 5 & 7: Cross out their multiples.
- The numbers left are your primes!
The Sieve of Eratosthenes: An Ancient Shortcut
Over 2,000 years ago, a Greek mathematician Eratosthenes invented a “sieve” to catch primes. Instead of checking every single number one by one, he found a way to “filter out” the non-primes (composite numbers).
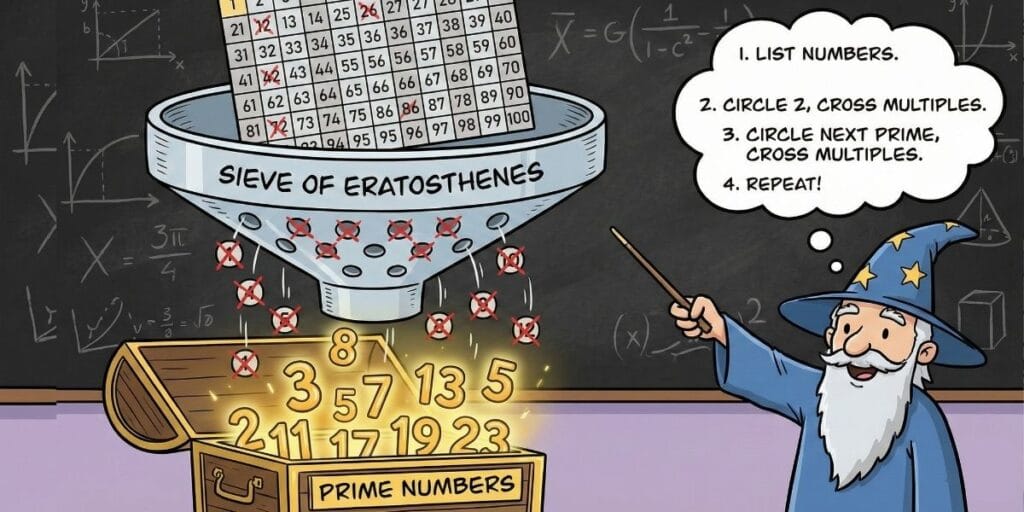
Here is how you can use the Sieve of Eratosthenes to find primes up to 100:
- List the Numbers: Write down all integers from 2 to 100. (We skip 1 because it isn’t prime!)
- Start with 2: Circle 2 (it’s the first prime) and cross out every other number after it (4, 6, 8, 10…). These are all multiples of 2, so they can’t be prime.
- Move to 3: Circle 3 (the next prime) and cross out all its multiples that aren’t already gone (9, 15, 21…).
- Keep Going: Move to the next unmarked number, which is 5. Circle it and cross out all multiples of 5 (25, 35, 55…).
- Final Filter: Do the same for 7. Once you reach the number 10 (the square root of 100), any number left unmarked is a Prime Number!
Author’s Message
“Mathematics is often taught as a series of rules to memorize, but I’ve always believed that understanding the ‘why’ is what makes it stick. While researching this guide, I looked at dozens of resources to identify where students and aspirants get stuck like the confusion between prime and composite numbers or the trickiness of the 80–100 range.
My goal with this article was to move beyond a simple list and provide you with a logical toolkit. Whether you’re preparing for a competitive exam or helping a child with their homework, I hope this guide makes the world of prime numbers feel a little less like a mystery and a lot more like a puzzle you’ve already solved.”
– Sahil
Read More:-
Conclusion
Prime numbers are much more than just a list of digits to memorize; they are the mathematical DNA of our number system. From the only even prime, 2, to the largest two-digit prime, 97, these 25 numbers between 1 and 100 form the foundation of everything from basic fractions to high-level computer encryption.
By understanding the Sieve of Eratosthenes and recognizing patterns like Twin Primes, you’ve moved beyond simple memorization. You now have a mental toolkit to identify these numbers quickly a skill that is invaluable for school exams, competitive tests, and logical problem-solving.
Frequently Asked Questions (FAQ’s)
Q1. Wait, why is 1 not a prime number?
This is the most common question! For a number to be prime, it must have exactly two factors (1 and itself). Since 1 only has one factor (itself), it doesn’t meet the criteria.
Q2. Is 0 a prime number?
No. Prime numbers must be positive integers greater than 1. 0 is a special number, but it’s not prime.
Q3. How many prime numbers are there between 1 and 100?
There are exactly 25 prime numbers. Remembering this “25” count is a great trick for competitive exams.
Q4. What is the largest prime number under 100?
The largest prime number before you hit 100 is 97.
Q5. Are all odd numbers prime?
Definitely not! Look at 9, 15, or 21. They are odd, but you can divide them by 3 or 7. Only specific odd numbers are prime.
